Завдання №1 (прийом відповідей до 02 грудня 2019 року)
|
Чи не змогли б ви, розставити плюси та мінуси між цифрами, так щоб вийшла рівність? |
Відповідь на завдання №1: Коли я подумав про це завдання, мені здавалося, що воно має одне рішення: 123 – 45 – 67 + 89 = 100 З вашою допомогою з’ясувалося, що є ще шість(!) можливих рішень: 1 + 23 – 4 + 56 + 7 + 8 + 9 = 100 12 + 3 + 4 + 5 – 6 – 7 + 89 = 100 12 – 3 – 4 + 5 – 6 + 7 + 89 = 100 123 – 4 – 5 – 6 – 7 + 8 – 9 = 100 1 + 2 + 3 – 4 + 5 + 6 + 78 + 9 = 100 123 + 4 – 5 + 67 – 89 = 100 |
Нами було отримано 38 відповідей, із них 32 були правильними.
Правильні відповіді надіслали (школи почергово):
- Геннадій Аронов, Марія Павленко, Вікторія Куляк, Олександр Урсу, Юрій Мирон, Олександр Сахаров із Технологічного ліцею ОРТ ім. Герцля, Кишинів, Молдова;
- Назар Алісултанов, Назар Шапіро, Аліса Скаповська, Саміра Абдуллаєва, Каріна Луньова, Софія Кролевич, Талля Айдарова, Маргарита Лавриненко, Софія Єрмошкіна з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Діана Тарханова, Ліана Балкова, Ганна Сечина, Артем Рімарчук, Софія Карватовська, Єгор Жоров, Анастасія Мартіросова з НВК №141, Київ, Україна;
- Данило Суханов, Ірина Охота, Матвій Кушпар із гімназії “ОРТ Алеф”, Запоріжжя, Україна;
- Марік Войцеховський, Дар’я Абраменко, Лірон Бланк із гімназії ім. Шалом Алейхема, Вільнюс, Литва;
- Ар’є Шафран, Ілля Кузміч з Єврейської школи, Таллінн, Естонія,
- Олександр Голецек із ЗОШ №41, Чернівці, Україна.
- Особливо хочеться відзначити Ганну Сечину з НВК №141, Київ, Україна , яка надіслала 2 різні та правильні рішення.
Завдання №2 (прийом відповідей до 09 грудня 2019 року)
| Перед нами квадратний аркуш паперу розміром 10 див на 10 див. Як нам (не розрізаючи і не користуючись лінійкою та іншими інструментами!) одержати з нього квадратний листок паперу, площа якого буде 50 см 2 ? |
Відповідь на завдання №2: У цьому квадратному листку ABCD загнемо кут A по лінії FE до центру. Те саме зробимо з іншими кутами B, C і D: 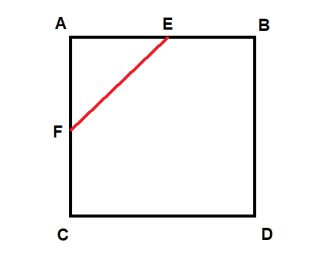 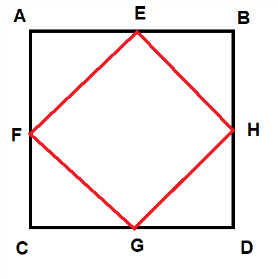 Площа отриманого квадрата FEHG дорівнює 50 см2 . |
Нами було отримано 24 рішення, з яких 20 виявились правильними. Правильні рішення надіслали (школи почергово):
- Анастасія Арнаутова із Технологічного ліцею ОРТ ім. Герцля, Кишинів, Молдова;
- Микита Даниленко, Назар Шапіро, Султан Станбеков, Микита Земляний, Назар Алісултанов, Василина Короткова, Гедалья Айдаров та Давид Міркін з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Валерія Скакун, Аскольд Гальчук та Поліна Грушевата із ЗОШ №41, Чернівці, Україна;
- Ілля Кузьмич та Даніель Богович з Єврейської школи, Таллінн, Естонія;
- Софія Карватовська, Валерія Швачка, Ганна Сечина та Лев Карпук із НКВ №141, Київ, Україна;
- Рон Кріхелі і Давид Циткілов зі школи №1311, Москва, Росія.
- Особливо хочеться відзначити Валерію Скакун, Аскольда Гальчука, Поліну Грушевату (всі із ЗОШ №41, Чернівці, Україна); Назара Шапіро, Султана Станбекова, Микиту Земляного, Назара Алісултанова, Василіну Короткову, Гедаллю Айдарова, Давида Міркіна (усі з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан); Ганну Сечину, Валерію Швачку, Лева Карпука (з НКВ №141, Київ, Україна); Рона Кріхелі, Давида Циткілова (зі школи №1311, Москва, Росія) за надіслані файли з поясненням їхнього вирішення. Вони отримали за це додаткові бали.
Завдання №3 (прийом відповідей до 16 грудня 2019 року)
Серед мешканців селища Маленьке є 1000 осіб, які мають свої машини. У кожної машини свій тризначний номер, починаючи від 000 до 999. Через гострий дефіцит бензину рада селища прийняла такі правила щодо заправки машин:
Пан Лакі живе у селищі Маленький і має машину. Коли він уважно прочитав нові правила про заправку машин, він сказав “Це цікаво, я можу заправити свою машину в будь-який день тижня!”. Який номер машини у пана Лакі? |
Розв’язання задачі №3 Позначимо суму чисел номера машини пана Лакі літерою Х. 1. За правилом №3 Х> 10, а за правилом №5 Х< 15 , тобто 10< X< 15. 2. За правилом №4 номер машини має ділитися на три, тобто Х має ділитися на три. Єдине число, яке задовольняє умовам 1 і 2, це 12, тобто Х = 12 і сума цифр номера машини дорівнює 12. За правилом №2 число має бути непарним і за правилом №1 усі цифри мають бути меншими за 6 – отже, останньою цифрою номера машини можуть бути 1, 3 або 5. За правилом №6 у номері мають бути хоча б дві однакові цифри. Разом з тим, що сума всіх цифр має бути 12 і всі цифри менші за 6 – номер машини не може закінчуватися на 1 (максимальна сума тоді буде 5 + 5 + 1 = 11)< 12). Якщо номер закінчується на 3, то тоді можливі номери 363 або 633, але так як всі цифри повинні бути менше 6 ці можливості теж відпадають. Значить, номер машини закінчується на 5, і ми маємо дві можливості 525 або 255. За правилом №7 номер машини має бути меншим за 500, значить номер машини пана Лакі, який задовольняє всі правила, – 255. |
Було отримано 41 рішення, з яких 27 виявилися правильними. Правильні рішення (школи почергово):
- Данило Авраменко, Максим Вацко та Ганна Сєчкіна з НКВ №141, Київ, Україна;
- Лірон Бланк із гімназії ім. Шалом Алейхема, Вільнюс, Литва;
- Олександра Гольдіна, Валерія Скакун та Аскольд Гальчук із ЗОШ №41, Чернівці, Україна;
- Ілля Кузьмич, Даніель Богович та Михайло Осипчик з Єврейської школи, Таллінн, Естонія;
- Віктор Сухоруков та Давид Циткілов зі школи №1311, Москва, Росія;
- Евеліна Грязєва з гімназії “ОРТ Алеф”, Запоріжжя, Україна;
- Назар Алісултанов, Назар Шапіро, Гедалья Айдаров, Султан Станбеков, Давид Міркін, Лія Тюлегенова та Талля Айдарова з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Арсеній Зайков, Даніель Лотоха, Михайло Лисянський, Гліб Леницький, Кіра Шварц, Анастасія Танська та Ганна Берлін із СШ “ОРТ” №94, Одеса, Україна.
Особливо хочеться відзначити Олександру Гольдіну (з ЗОШ №41, Чернівці, Україна) та Давида Міркіна (з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан) за надіслані файли з гарним поясненням їх вирішення.
На жаль, не всі учасники зрозуміли систему нарахування балів, і ми отримали багато правильних відповідей без жодного пояснення. У цьому турі, ми вирішили дати 3 бали за правильну відповідь та 4 бали за відповідь з гарним рішенням та поясненням.
Завдання №4 (прийом відповідей до 23 грудня 2019 року)
| Група з 12 осіб (чоловіків, жінок та дітей) несе 12 буханок хліба. Кожен чоловік несе 2 буханки, кожна жінка несе 1/2 буханки і кожна дитина несе 1/4 буханки хліба. Скільки було у групі чоловіків, жінок та дітей? |
Розв’язання задачі №4
Позначимо число чоловіків у групі літерою Х, число жінок літерою Y та число дітей літерою Z. |
Нами було отримано 25 відповідей, з яких 22 виявились правильними.
Правильні відповіді (школи почергово) надіслали:
- Давид Циткілов та Захар Манеліс зі школи №1311, Москва, Росія;
- Ілля Кузьмич та Даніель Богович з Єврейської школи, Таллінн, Естонія;
- Ганна Сєчкіна, Данило Авраменко та Єгор Жоров із НКВ №141, Київ, Україна;
- Лірон Бланк та Марік Войцеховський з гімназії ім. Шалом Алейхема, Вільнюс, Литва;
- Матвій Кушпар із гімназії “ОРТ Алеф”, Запоріжжя, Україна;
- Олександр Голецек із ЗОШ №41, Чернівці, Україна;
- Гедалья Айдаров та Назар Шапіро з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Усі вони одержують по 1 балу.
Відповіді з неповним рішенням (школи почергово) надіслали:
- Максим Вацко та Костя Єрьомін з НКВ №141, Київ, Україна;
- Аскольд Гальчук та Поліна Грушевата із ЗОШ №41, Чернівці, Україна;
- Євгенія Ліфшиць зі школи ім. Дубнова, Рига, Латвія;
- Назар Алісултанов та Маргарита Лавриненко з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Усі вони отримують по 2 бали .
Повне рішення надіслали:
- Валерія Скакун із ЗОШ №41, Чернівці, Україна;
- Давид Міркін з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Вони одержують по 3 бали.
Особливо хочеться відзначити Олександру Гольдіну із ЗОШ №41, Чернівці, Україна за оригінальне (але неповне) рішення, вона отримує додатковий бонусний бал (всього 3 бали).
Завдання №5 (прийом відповідей до 30 грудня 2019 року)
| Після 7 прання шматок господарського мила став удвічі коротшим, удвічі вужчим й удвічі нижчим.
На скільки застосувань вистачить шматка, що залишився? |
Розв’язання задачі №5
Позначимо довжину шматка мила спочатку буквою а, ширину шматка мила спочатку буквою b і висоту шматка мила спочатку буквою с. |
Нами було отримано 14 відповідей, з яких 11 виявились правильними.
Правильні відповіді (школи почергово) надіслали:
- Назар Алісултанов з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Єгор Жоров із НКВ №141, Київ, Україна;
Обидва одержують по 1 балу.
Відповідь з неповним рішенням надіслав:
- Ілля Кузьмич із Єврейської школи, Таллінн, Естонія;
Він отримує 2 бали .
Повне рішення надіслали:
- Аскольд Гальчук, Валерія Скакун та Олександра Гольдіна із ЗОШ №41, Чернівці, Україна;
- Маргарита Лавриненко, Дар’я Непомнящая, Назар Шапіро та Давид Міркін з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Усі вони отримують по 3 бали.
Особливо хочеться відзначити за творчу подачу свого рішення Костю Єрьоміна з НКВ №141, Київ, Україна. Він отримує додатковий бонусний бал (всього 4 бали).
Завдання №6 (прийом відповідей до 20 січня 2020 року)
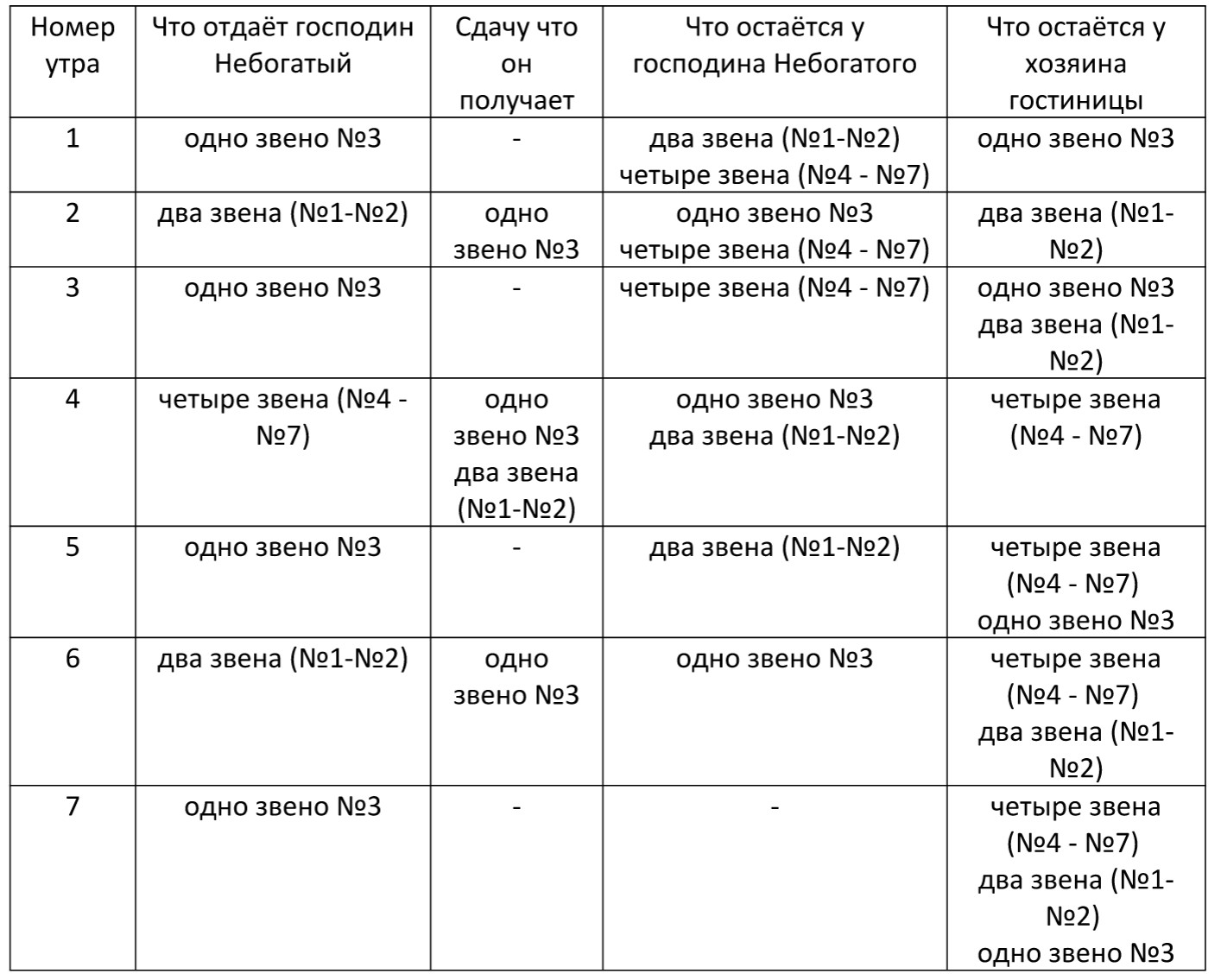
| Пан Небагатий приїхав до міста у справах, він мав залишитись там на 8 днів (7 ночей). У місті був один готель, але грошей у нього не було. Зате у нього був гарний срібний ланцюжок із 7 ланок.
Хазяїну готелю ланцюжок сподобався, і вони домовилися, що пан Небагатий розплатиться ланцюжком за своє проживання у готелі. Але оскільки оплата в готелі щоденна господар висунув такі вимоги: 1. щоранку пан Небагатий повинен віддати йому одну ланку ланцюжка, як оплату за минулу ніч Як пан Небагатий повинен виконати ці умови і скільки розрізів потрібно для цього зробити? |
Відповідь на завдання:
Для того, щоб виконати умови господаря готелю та прожити там 7 ночей, пан Небагатий має зробити один розріз ланки №3:
Після цього ланцюжок розпадеться на три частини – одна ланка №3 (яка була розрізана), дві зв’язані ланки (№1 і №2) і чотири зв’язані ланки (№4 – №7).
Число ланок ланцюжка, які залишаються у господаря щоранку, дорівнює кількості ночей, які провів пан Небагатий у його готелі. |
Нами було отримано 13 рішень , з яких 5 виявилися повними та правильними.
Правильні рішення (школи почергово) надіслали:
- Назар Алісултанов, Аліса Скоповська, Назар Шапіро та Давид Міркін з Єврейської
школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан; - Валерія Скакун із ЗОШ №41, Чернівці, Україна;
Усі вони отримують по 3 бали .
Завдання №7 (прийом відповідей до 27 січня 2020 року)
| Один хлопчик вирішив принести своїй бабусі кілька тістечок на честь дня народження. Бабуся живе в іншому кінці міста і дорогою до неї потрібно пройти 7 мостів. На кожному мосту живе голодний Сірий Вовк, він відбирає у хлопчика половину тістечок, які має. Але якщо хлопчик розповість йому, що ці тістечка призначені для бабусі, у якої сьогодні День народження, Сірий Вовк його пошкодує і віддасть йому тістечко назад.Скільки тістечок хлопчик має взяти з собою з дому для того, щоб принести бабусі два тістечка? |
Розв’язання задачі №7
Почнемо розв’язання задачі з кінця – хлопчику треба піти з сьомого мосту із двома тістечками. На цьому мості, одне тістечко він отримав від Сірого Вовка (після того, як віддав йому половину того, що в нього було), значить він прийшов на цей міст з двома тістечками – одне він відразу віддав Сірому Вовку, а потім, розповівши йому про бабусю, отримав одне тістечка назад. Тобто якщо хлопчик приходить на кожен міст із двома тістечками, одне він спочатку віддає, а потім отримує його назад. В результаті він і йде з цього мосту з двома тістечками. Тому найкраще для нього рішення це вийти з дому з двома тістечками і на кожному мосту розповідати Сірому Вовку, що це тістечка для бабусі, у якої сьогодні День народження. |
Як правильно помітили Давид Міркін і Дар’я Непомнящая (з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан), завдання має й інші рішення. Ці рішення є не найкращими. Так наприклад, якщо хлопчик не буде просити тістечка назад, він може вийти з дому з 256 ( 28 = 256), на кожному мосту віддати половину і прийти до бабусі з 2 тістечками. В принципі, можна довести, що вийшовши з дому з будь-якою кількістю тістечок більше двох, (і просячи тістечка назад) у хлопчика в кінці залишиться більше двох тістечок.
Нами було отримано 16 відповідей та рішень , з яких 14 виявилися правильними.
- Правильну відповідь надіслав Данило Авраменко з НКВ №141, Київ, Україна; він одержує один бал.
Правильну відповідь із неточним рішенням надіслали:
- Матвій Кушпар та Данило Суханов з гімназії “ОРТ Алеф”, Запоріжжя, Україна.
Кожен учень отримує два бали.
Правильні відповіді з повним рішенням (школи почергово) надіслали:
- Даніель Богович та Ілля Кузьмич з Єврейської школи, Таллінн, Естонія;
- Евеліна Грязєва з гімназії “ОРТ Алеф”, Запоріжжя, Україна;
- Назар Алісултанов, Аліса Скоповська, Давид Міркін та Назар Шапіро з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Валерія Скакун та Аскольд Гальчук із ЗОШ №41, Чернівці, Україна;
- Костя Єрьомін із НКВ №141, Київ, Україна;
Усі вони отримують по 3 бали.
Хочеться відзначити Дар’ю Непомнящую з Єврейської школи “ОРТ Прі Ец Хаїм” , Бішкек, Киргизстан, яка надіслала додаткове можливе рішення. На жаль, у цьому рішенні виявилася помилка, і вона також отримує 3 бали.
Завдання №8 (прийом відповідей до 03 лютого 2020 року)
| П’ять добрих друзів пішли погуляти. По дорозі вони трохи зголодніли, але мали один великий бублик.
Так як всі були хорошими друзями, і в різній мірі голодні, вони не заперечували отримати різного розміру шматочки, але при цьому вони хотіли розділити бублик за допомогою всього двох розрізів. |
Розв’язання задачі №8 Для правильного вирішення є дві умови:
|
Нами було отримано 16 рішень, з яких 12 виявились правильними.
Правильні рішення (школи почергово) надіслали:
- Валерія Скакун, Поліна Гушевата та Аскольд Гальчук із ЗОШ №41, Чернівці, Україна;
- Бенайа Айдаров, Аліса Скоповська, Софія Мірошкіна, Давид Міркін, Назар Шапіро та Султан Станбеков з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Усі вони отримують по 3 бали.
Деякі учні правильно вказали на умову №1 (перетин розрізів на самому бублику), але до правильного формулювання другої умови найближче підійшли:
- Даніель Богович та Ілля Кузьмич з Єврейської школи, Таллінн, Естонія;
Ганна Сєчкіна з НКВ №141, Київ, Україна;
Вони отримують додатковий бонусний бал та всього по 4 бали.
Завдання №9 (прийом відповідей до 10 лютого 2020 року)
| У країні Тімбокту в ході монети 1 тимбоку, 3 тимбоку та 5 тимбоку.
Чи зможете ви розміняти паперову купюру в 200 тимбоку на монети, щоб загальна кількість монет була непарною? |
Розв’язання задачі №9:
Позначимо число монет номіналом 1 тимбоку як k, номіналом 3 тимбоку як m і номіналом 5 тимбоку як n. Зрозуміло що k, m, n цілі та невід’ємні числа. |
Нами було отримано 11 відповідей та рішень, з яких 10 виявилися правильними.
Правильну відповідь надіслав:
- Даніель Богович із Єврейської школи, Таллінн, Естонія; Він отримує 1 бал.
Правильну відповідь із частковим рішенням (школи почергово) надіслали:
- Ілля Кузьмич із Єврейської школи, Таллінн, Естонія;
- Назар Алісултанов, Султан Станбеков, Дар’я Непомняща з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Костя Єрьомін з НКВ №141, Київ, Україна;
Усі вони отримують по 2 бали.
Повні рішення надіслали:
- Давид Міркін та Назар Шапіро з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Валерія Скакун із ЗОШ №41, Чернівці, Україна;
На жаль, рішення Давида Міркіна було не зовсім точним і він отримує 2 бали. Назар Шапіро з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан та Валерія Скакун із ЗОШ №41, Чернівці, Україна отримують по 3 бали за свої рішення.
Гарний доказ неможливості розміну надіслала Аліса Скоповська з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан. Вона отримує додатковий бонусний бал та всього 4 бали.
Завдання №10 (прийом відповідей до 17 лютого 2020 року)
Ювелір, механік та інженер імена яких (не обов’язково в порядку їхніх професій!) Борис, Льова та Мишко зустрілися з аеропорту на шляху до Тімбокту на літню відпустку. Із загальної розмови з’ясувалося що:
Як звати ювеліра? |
Розв’язання задачі №10 1. Якщо Борис і механік жили колись у селищі Маленький, то Борис не механік . 2. Якщо ювелір та Льова живуть в одній країні, значить Льова не ювелір 3. Якщо Михайло молодший за інженера, значить Михайло не інженер 4. Якщо Льова старше механіка, значить Льова не механік Якщо Льова не ювелір і не механік, значить Льова інженер. Борис не механік і інженер, значить Борис ювелір. Відповідь – ювеліра звуть Борис. |
Нами було отримано 14 відповідей та рішень, з яких 13 виявились правильними.
Правильну відповідь надіслав:
- Єгор Жоров із НКВ №141, Київ, Україна;
Він отримує 1 бал.
Правильну відповідь із повним рішенням (школи почергово) надіслали:
- Ілля Кузьмич та Даніель Богович з Єврейської школи, Таллінн, Естонія;
- Назар Шапіро, Софія Єрмошкіна, Назар Алісултанов, Аліса Скоповська, Давид Міркін, Дар’я Непомняща з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Валерія Скакун, Поліна Гушовата та Олександра Гольдіна із ЗОШ №41, Чернівці, Україна;
- Костя Єрьомін із НКВ №141, Київ, Україна;
Усі вони отримують по 3 бали.
Завдання №11 (прийом відповідей до 24 лютого 2020 року)
| Під час стоянки маленького корабля між двома рейсами матросу виповнилося 20 років. З цієї нагоди у каюті зібралися усі 6 членів команди. Я вдвічі старший за юнгу і на 6 років старший за машиніста – сказав керманич. А я на стільки ж років старший за юнгу, на скільки молодший за машиніста – зауважив боцман. Крім того я на 4 роки старший за матроса. Ви знаєте, що середній вік усієї нашої команди 28 років – сказав капітан. Скільки років капітанові? |
Відповідь на завдання №11: Матросу 20 років, і якщо боцман на 4 роки його старший, це означає що боцману 24 роки. Визначимо вік юнги за Х, а вік машиніста за Y. За словами боцмана він на стільки ж років старший за юнгу наскільки молодший за машиніста, значить: 24 – Х = Y – 24 За словами рульового він вдвічі старший за юнгу і на 6 років старший за машиніста, значить: 2Х = Y + 6 У нас є 2 рівняння з двома невідомими: Х + Y = 48 2Х – Y = 6 Складемо ці два рівняння та отримаємо 3Х = 54 та Х = 18. Підставимо Х у перше рівняння та отримаємо Y = 30. Тобто юнзі 18 років, машиністу 30 років, а керманичу 36 років. Сума віку юнги, матроса, боцмана, машиніста та рульового: 18 + 20 + 24 + 30 + 36 = 128 Середній вік усіх 6 членів команди 28 років, тому сума їх віку має бути 28 х 6 = 168 Тому вік капітана 168 – 128 = 40 років. |
Нами було отримано 9 правильних відповідей та рішень.
Правильну відповідь надіслала:
- Софія Єрмошкіна з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан; Вона отримує 1 бал.
Правильну відповідь з неповним рішенням надіслав:
- Ілля Кузьмич із Єврейської школи, Таллінн, Естонія; Він отримує 2 бали.
Правильну відповідь з повним рішенням надіслав:
- Костя Єрьомін із НКВ №141, Київ, Україна;
На жаль, у його рішенні була помилка і він отримує також 2 бали.
Правильну відповідь із повним рішенням (школи почергово) надіслали:
- Назар Шапіро, Аліса Скоповська та Давид Міркін з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Валерія Скакун та Поліна Гушувата із ЗОШ №41, Чернівці, Україна;
- Михайло Панасюк із НКВ №141, Київ, Україна;
Усі вони отримують по 3 бали.
Завдання №12 (прийом відповідей до 02 березня 2020 року)
| По дереву заввишки 14 метрів повзе гусінь. За день вона піднімається на 6 метрів нагору, а за ніч сповзає на 4 метри вниз.
Якщо гусінь почала повзти із землі, за скільки днів вона потрапить на вершину дерева? |
Відповідь на завдання №12:
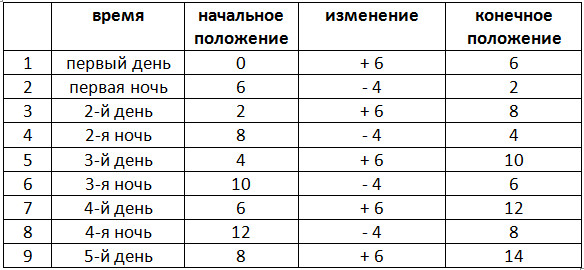
Опишемо положення гусені в наступній таблиці (всі відстані в метрах):
Так як висота дерева 14 метрів, гусінь потрапить на вершину наприкінці п’ятого дня. |
Нами було отримано 14 відповідей та рішень, з яких 11 виявилися правильними.
Правильну відповідь надіслав:
- Єгор Жоров із НКВ №141, Київ, Україна; Він отримує 1 бал.
Правильну відповідь із повним рішенням (школи почергово) надіслали:
- Данило Суханов з гімназії “ОРТ Алеф”, Запоріжжя, Україна;
- Яша Доля та Іван Марков із Технологічного ліцею ОРТ імені Б. З. Герцля, Кишинів, Молдова;
- Назар Шапіро, Аліса Скоповська, Давид Міркін та Дар’я Непомнящая з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Аскольд Гальчук, Валерія Скакун та Олександра Гольдіна із ЗОШ №41, Чернівці, Україна;
Усі вони отримують по 3 бали.
Завдання №13 (прийом відповідей до 09 березня 2020 року)
| Електропотяг завдовжки 20 метрів проїжджає повз кілометровий стовп за 2 секунди.
Якщо швидкість поїзда стала, то скільки часу йому знадобиться, щоб проїхати міст завдовжки 40 метрів? |
Відповідь на завдання №13:
Так як поїзд завдовжки 20 метрів, проїжджає повз стовп за 2 секунди, швидкість поїзда: 20 м/2 сек = 10 м/сек Для того, щоб повністю проїхати міст завдовжки 40 метрів, локомотив поїзда повинен проїхати 60 метрів (40 метрів довжина моста + 20 метрів довжина поїзда). Оскільки швидкість поїзда 10 м/сек це займе: 60 м / 10 м/сек = 6 секунд |
Нами було отримано 12 відповідей та рішень, з яких 9 виявилися правильними.
Повне рішення з маленькою помилкою надіслали:
- Яша Частка із Технологічного ліцею ОРТ імені Б. З. Герцля, Кишинів, Молдова;
- Лія Тюлегенова з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Вони одержують по 2 бали.
Правильну відповідь із повним рішенням (школи почергово) надіслали:
- Назар Шапіро, Дар’я Непомнящая, Аліса Скоповська та Давид Міркін з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Ілля Кузьмич із Єврейської школи, Таллінн, Естонія;
- Валерія Скакун із ЗОШ №41, Чернівці, Україна;
- Костя Єрьомін із НКВ №141, Київ, Україна;
Усі вони отримують по 3 бали.
Завдання №14 (прийом відповідей до 16 березня 2020 року)
| Натуральне число називається паліндромом, якщо його значення не змінюється, коли ми читаємо зправа наліво. Так, наприклад, 12321 це паліндром, а 123456 – ні.
Перед вами приклад додавання: ** + *** = **** (кожна зірочка позначає якусь цифру), в якій обидва доданки та їх сума є паліндромами. Чи не змогли б ви знайти рішення цього прикладу? |
Рішення задачі:
Нам відомо що ** + *** = **** (кожна зірочка позначає якусь цифру) та обидва доданки та їх сума є паліндромами. Зрозуміло, що сума двозначного та тризначного чисел буде виду 1aa1. Для того, щоб отримати в сумі число більше 1000, тризначне число може бути лише виду 9b9. Тобто ** + 9b9 = 1aa1. Тому двозначне число може бути лише 22 і ми маємо 22 + 9b9 = 1aa1. Зараз є три можливості для цифри b: b = 7, b = 8 або b = 9. Якщо b = 7, то ми отримуємо 22 + 979 = 1001 і всі числа паліндроми. Якщо b = 8, то ми отримуємо 22 + 989 = 1011 і сума не є паліндромом. Якщо b = 9 ми отримуємо 22 + 999 = 1021 і сума знову є паліндромом. Тому єдине рішення, яке виконує всі умови: 22 + 979 = 1001 |
Нами було отримано 12 відповідей та рішень і всі вони виявились правильними.
- Правильну відповідь надіслали:
Даніель Богович та Ілля Кузьмич з Єврейської школи, Таллінн, Естонія;
Каріна Луньова з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Єгор Жоров із НКВ №141, Київ, Україна;
Усі вони одержують по 1 балу. - Часткове рішення надіслала:
Лія Тюлегенова з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Вона отримує 2 бали. - Правильну відповідь із повним рішенням (школи почергово) надіслали:
Назар Шапіро, Назар Алісултанов, Аліса Скоповська та Давид Міркін з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Костя Єрьомін із НКВ №141, Київ, Україна;
Валерія Скакун та Олександра Гольдіна із ЗОШ №41, Чернівці, Україна;
Усі вони отримують по 3 бали.
Завдання №15 (прийом відповідей до 23 березня 2020 року)
| Перед нами три закриті коробочки, у кожній лежить одна маленька кулька біла, чорна або зелена. На кожній коробочці є напис: “білий”, “чорний”, “або білий або зелений”, але жоден з написів не відповідає вмісту.
Не змогли б ви визначити, яка кулька знаходиться в кожній коробочці? |
Розв’язання задачі 15:
Нам відомо що:
Крім того, ми знаємо, що всі написи неправильні, тому в коробочці №3 («або біла або зелена») може знаходитися тільки чорна кулька:
Тоді біла кулька має бути в коробочці №2 на якій написано «чорна», а зелена кулька буде тоді в коробочці №1.
|
Нами було отримано 12 відповідей та рішень, з них 10 виявилися правильними.
Повні правильні рішення (школи почергово) надіслали:
- Валерія Скакун та Олександра Гольдіна із ЗОШ №41, Чернівці, Україна;
- Каріна Луньова, Аліса Скоповська, Назар Алісултанов, Давид Міркін та Назар Шапіро з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Костя Єрьомін із НКВ №141, Київ, Україна;
- Іван Марков із Технологічного ліцею ОРТ імені Б. З. Герцля, Кишинів, Молдова;
- Ілля Кузьмич із Єврейської школи, Таллінн, Естонія;
Усі вони отримують по 3 бали.
Завдання №16 (прийом відповідей до 30 березня 2020 року)
| Учень купив 4 різні зошити. Всі зошити без першого коштують 42 гривені, всі без другого – 40 гривень, усі без третього – 38 гривень і всі без четвертого – 36 гривень.
Скільки коштує кожен зошит? |
Рішення задачі:
Позначимо вартості зошитів: Х 1 – перший зошит, Х 2 – другий зошит, Х 3 – третій зошит, Х 4 – четвертий зошит За умовами завдання ми зможемо скласти такі рівняння:
У нас є проста система із чотирьох рівнянь із чотирма невідомими, і є кілька способів її вирішити. Найпростіший це скласти всі рівняння, ми отримаємо: 3Х 1 + 3Х 2 + 3Х 3 + 3Х 4 = 156 або 3(Х 1 + Х 2 + Х 3 + Х 4 ) = 156 ; розділимо на 3 та отримаємо: Х 1 + Х 2 + Х 3 + Х 4 = 52 Тобто вартість усіх чотирьох зошитів 52 гривні. Тому вартість кожного зошита:
|
Нами було отримано 10 відповідей та рішень, усі вони виявилися правильними.
- Правильну відповідь, але без пояснення надіслала Даана Салієва з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан; Вона отримує 1 бал.
Повні правильні рішення (школи почергово) надіслали:
- Ілля Кузьмич із Єврейської школи, Таллінн, Естонія;
- Валерія Скакун із ЗОШ №41, Чернівці, Україна;
- Дар’я Непомняща, Аліса Скоповська, Назар Шапіро, Лія Тюлегенова, Давид Міркін та Назар Алісултанов з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Костя Єрьомін із НКВ №141, Київ, Україна;
Усі вони отримують по 3 бали.
Завдання №17 (прийом відповідей до 06 квітня 2020 року)
| Іра, Даша, Мишко та Боря збирали гриби у лісі.
Іра зібрала найбільше грибів, а Даша не найменше. Чи правда, що дівчатка зібрали більше грибів, ніж хлопчики? |
Рішення задачі:
Позначимо скільки грибів зібрав кожен із хлопців: Х 1 – Іра, Х 2 – Даша, Y 1 – Мишко, Y 2 – Боря За умовами завдання ми знаємо що Іра зібрала найбільше грибів, а Даша не менше всіх. Тобто Х 1> Х 2 , Y 1 , Y 2 і ми маємо кілька можливостей:
Тоді може бути Х 2 ≥ Y 1> Y 2 або Y 1> Х 2 ≥ Y 2 У будь-якому з цих випадків так як Х 1> Y 1 і Х 2 ≥ Y 2 то Х 1 + Х 2> Y 1 + Y 2
Тоді знову може бути Х 2> Y 1 = Y 2 або Х 2 = Y 1 = Y 2 У кожному з цих випадків Х 2 ≥ Y 1 = Y 2 І тому знову, бо Х 1> Y 1 і Х 2 ≥ Y 2 то Х 1 + Х 2> Y 1 + Y 2 Тобто у будь-якому разі дівчатка зібрали більше грибів, ніж хлопчики. |
Нами було отримано 9 відповідей та рішень, усі вони виявилися правильними.
Правильну відповідь, але без рішення надіслала Даана Салієва з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Правильну відповідь (з не дуже зрозумілим поясненням) надіслав Костя Єрьомін із НКВ №141, Київ, Україна;
Вони одержують по 1 балу.
Повні правильні рішення (школи почергово) надіслали:
Аліса Скоповська, Давид Міркін, Назар Шапіро, Назар Алісултанов та Дар’я Непомнящая з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Даніель Богович із Єврейської школи, Таллінн, Естонія;
Валерія Скакун із ЗОШ №41, Чернівці, Україна;
Усі вони отримують по 3 бали.
Завдання №18 (прийом відповідей до 13 квітня 2020 року)
| У льоху 20 однакових на вигляд банок із варенням. У 8 банках полуничне варення, у 7 банках малинове варення та у 5 банках вишневе варення.
Яка найбільша кількість банок, які можна винести в темряві з льоху з упевненістю, що там залишилися хоча б ще 4 банки одного сорту варення та 3 банки іншого сорту? |
Рішення задачі:Для вирішення завдання повинні дотримуватися двох умов:
Для опису ситуації введемо позначення – (кількість банок полуничного варення, кількість банок малинового варення, кількість банок вишневого варення). Наше початкове становище – (8, 7, 5). Зрозуміло що ми не можемо забрати з льоху 12 банок варення, тому що може статися, що ми візьмемо всі банки малинового та вишневого варення і тоді вийде:
Якщо ми спробуємо взяти 11 банок, може вийде:
Якщо ми спробуємо взяти 10 банок, може вийде:
Спробуємо взяти 9 банок, може вийде:
Спробуємо взяти 8 банок, може вийде:
Але якщо ми візьмемо 7 банок, легко переконуємося, що обидві умови будуть дотримані. Тому максимальна кількість банок варення, які можна взяти з льоху, дорівнює 7. |
Нами було отримано 7 рішень, всі вони виявились правильними.
Повні правильні рішення (школи почергово) надіслали:
Аліса Скоповська, Давид Міркін, Назар Алісултанов, Назар Шапіро та Дар’я Непомняща з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан; Валерія Скакун із ЗОШ №41, Чернівці, Україна;
Костя Єрьомін із НКВ №141, Київ, Україна;
Усі вони отримують по 3 бали.
Завдання №19 (прийом відповідей до 20 квітня 2020 року)
| У деяких натуральних чисел є цікава властивість: якщо ми помножимо це число на два, то ми отримаємо квадрат іншого числа, а якщо ми помножимо це число на три, то отримаємо куб ще одного числа.
Чи не змогли б ви знайти мінімальне натуральне число, у якого є така властивість? |
Рішення задачі:
Позначимо наше число як Х, тоді за умовами завдання: 2Х = n 2 і 3Х = s 3 (Х ≠ n; Х ≠ s) З останніх рівнянь зрозуміло, що n має ділитися на 2 та s має ділитися на 3. Тобто n = 2m та s = 3t; підставимо n і s у наші рівняння та отримаємо: 2Х = (2m) 2 тобто 2Х = 4m 2 і Х = 2 m 2 3Х = (3t) 3 тобто 3Х = 27t 3 та Х = 9 t 3 Ми отримали що: 2m 2 = 9t 3 ; з цього рівняння зрозуміло, що m має ділитися на 3 і t має ділитися на 2. Тобто m = 3k та t = 2u; підставимо ці m і t в останнє рівняння та отримаємо: 2(3k) 2 = 9(2u) 3 тобто 2(9k 2 ) = 9(8u 3 ) і після скорочень отримаємо k 2 = 4u 3 (*) Ми шукаємо мінімальне рішення даного рівняння у натуральних числах тому: k = 2 і u = 1, і тому m = 3k = 6 і t = 2u = 2 Х = 2m2 тобто Х = 2(6) 2 = 72 (або Х = 9 t 3 тобто Х = 9(2) 3 = 72) Цей метод розв’язання дозволяє знайти і наступні натуральні числа, що володіють цією властивістю. Так, наприклад, другим рішенням рівняння (*) буде k = 16 і u = 4 і відповідно m = 3k = 48 і Х = 2 m 2 тобто Х = 2 (48) 2 = 4608. Третім рішенням рівняння (*) буде k = 54 та u = 9 і відповідно m = 3k = 162 та Х = 2 m 2 тобто Х = 2 (162) 2 = 52 488 і так далі. |
Було отримано 7 відповідей та рішень, 6 з них виявились правильними.
Правильну відповідь (але без пояснення) надіслала: Дар’я Непомнящая з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан; Вона отримує 1 бал.
Правильну відповідь із частковим поясненням надіслали:
- Костя Єрьомін із НКВ №141, Київ, Україна;
- Назар Алісултанов з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
Вони одержують по 2 бали.
Правильні рішення з повним поясненням (школи почергово) надіслали:
- Назар Шапіро та Аліса Скоповська з Єврейської школи “ОРТ Прі Ец Хаїм”, Бішкек, Киргизстан;
- Олександра Гольдіна із ЗОШ №41, Чернівці, Україна;
Усі вони отримують по 3 бали.