Задание №1 (прием ответов до 02 декабря 2019)
|
Не смогли бы вы расставить плюсы и минусы между цифрами, так чтобы получилось равенство? |
Ответ на задачу №1: Когда я подумал об этой задаче, мне казалось что у неё одно решение: 123 – 45 – 67 + 89 = 100С вашей помощью выяснилось, что есть еще шесть(!) возможных решений: 1 + 23 – 4 + 56 + 7 + 8 + 9 = 100 12 + 3 + 4 + 5 – 6 – 7 + 89 = 100 12 – 3 – 4 + 5 – 6 + 7 + 89 = 100 123 – 4 – 5 – 6 – 7 + 8 – 9 = 100 1 + 2 + 3 – 4 + 5 + 6 + 78 + 9 = 100 123 + 4 – 5 + 67 – 89 = 100 |
Нами было получено 38 ответов, из них 32 были правильными.
Правильные ответы прислали (по школам в порядке очерёдности):
- Геннадий Аронов, Мария Павленко, Виктория Куляк, Александр Урсу, Юрий Мирон, Александр Сахаров из Технологического лицея ОРТ им. Герцля, Кишинёв, Молдова;
- Назар Алисултанов, Назар Шапиро, Алиса Скаповская, Самира Абдуллаева, Карина Лунева, София Кролевич, Талья Айдарова, Маргарита Лавриненко, Софья Ермошкина из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Диана Тарханова, Лиана Балкова, Анна Сечина, Артём Римарчук, Софья Карватовска, Егор Жоров, Анастасия Мартиросова из НВК №141, Киев, Украина;
- Даниил Суханов, Ирина Охота, Матвей Кушпарь из гимназии “ОРТ Алеф”, Запорожье, Украина;
- Марик Войцеховский, Дарья Абраменко, Лирон Бланк из гимназии им. Шалом Алейхема, Вильнюс, Литва;
- Арье Шафран, Илья Кузмич из Еврейской школы, Таллинн, Эстония,
- Александр Голецек из СШ №41, Черновцы, Украина.
- Особенно хочется отметить Анну Сечину из НВК №141, Киев, Украина, которая прислала 2 разных и правильных решения.
Задание №2 (прием ответов до 09 декабря 2019)
| Перед нами квадратный листок бумаги размером 10 см на 10 см. Как нам (не разрезая и не пользуясь линейкой и другими инструментами!) получить из него квадратный листок бумаги площадь которого будет 50 см2? |
Ответ на задачу №2: В данном квадратном листочке ABCD загнём угол A по линии FE к центру. То же самое сделаем с остальными углами B, C и D: 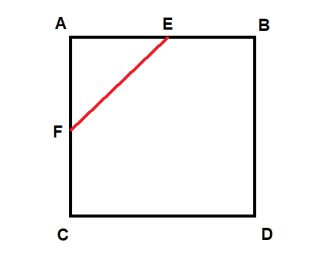 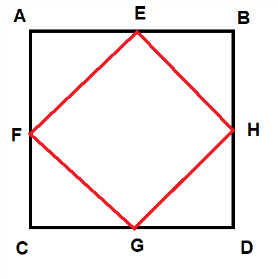 Площадь полученного квадрата FEHG равна 50 см2. |
Нами было получено 24 решения, из которых 20 оказались правильными. Правильные решения (по школам в порядке очерёдности прислали):
- Анастасия Арнаутова из Технологического лицея ОРТ им. Герцля, Кишинёв, Молдова;
- Никита Даниленко, Назар Шапиро, Султан Станбеков, Никита Земляной, Назар Алисултанов, Василина Короткова, Гедалья Айдаров и Давид Миркин из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Валерия Скакун, Аскольд Гальчук и Полина Грушевата из СШ №41, Черновцы, Украина;
- Илья Кузьмич и Даниэль Богович из Еврейской школы, Таллинн, Эстония;
- София Карватовска, Валерия Швачка, Анна Сечина и Лев Карпук из НКВ №141, Киев, Украина;
- Рон Крихели и Давид Циткилов из школы №1311, Москва, Россия.
- Особенно хочется отметить Валерию Скакун, Аскольда Гальчука, Полину Грушевату (все из СШ №41, Черновцы, Украина); Назара Шапиро, Султана Станбекова, Никиту Земляного, Назара Алисултанова, Василину Короткову, Гедалью Айдарова, Давида Миркина (все из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан); Анну Сечину, Валерию Швачка, Льва Карпука (из НКВ №141, Киев, Украина); Рона Крихели, Давида Циткилова (из школы №1311, Москва, Россия) за присланные файлы с объяснением их решения. Они получают за это по дополнительному баллу.
Задание №3 (прием ответов до 16 декабря 2019)
Среди жителей посёлка Маленький есть 1000 человек, которые имеют свои машины. У каждой машины свой трёхзначный номер, начиная от 000 и кончая 999. Из-за острого дефицита бензина совет посёлка принял следующие правила о заправке машин:
Господин Лаки живёт в посёлке Маленький и у него есть машина. Когда он внимательно прочитал все новые правила о заправке машин, он сказал “Это интересно, я могу заправить свою машину в любой день недели!”. Какой номер машины у господина Лаки? |
Решение задачи №3 Обозначим сумму чисел номера машины господина Лаки буквой Х. 1. По правилу №3 Х >10 , а по правилу №5 Х < 15 , то есть 10<X<15. 2. По правилу №4 номер машины должен делиться на три, то есть Х должен делиться на три. Единственное число, которое удовлетворяет условиям 1 и 2 это 12, то есть Х = 12 и сумма цифр номера машины равна 12. По правилу №2 число должно быть нечётным и по правилу №1 все цифры должны быть меньше 6 – значит, последней цифрой номера машины могут быть 1, 3 или 5. По правилу №6 в номере должны быть хотя бы две одинаковые цифры. Вместе с тем, что сумма всех цифр должна быть 12 и все цифры меньше 6 – номер машины не может заканчиваться на 1 (максимальная сумма тогда будет 5 + 5 + 1 = 11<12). Если номер заканчивается на 3 то тогда возможные номера 363 или 633, но так как все цифры должны быть меньше 6 эти возможности тоже отпадают. Значит, номер машины заканчивается на 5, и у нас есть две возможности 525 или 255. По правилу №7 номер машины должен быть меньше 500, значит номер машины господина Лаки, который удовлетворяет всем правилам, – 255. |
Было получено 41 решение, из которых 27 оказались правильными. Правильные решения (по школам в порядке очерёдности прислали):
- Данил Авраменко, Максим Вацко и Анна Сечкина из НКВ №141, Киев, Украина;
- Лирон Бланк из гимназии им. Шалом Алейхема, Вильнюс, Литва;
- Александра Гольдина, Валерия Скакун и Аскольд Гальчук из СШ №41, Черновцы, Украина;
- Илья Кузьмич, Даниэль Богович и Михаил Осипчик из Еврейской школы, Таллинн, Эстония;
- Виктор Сухоруков и Давид Циткилов из школы №1311, Москва, Россия;
- Эвелина Грязева из гимназии “ОРТ Алеф”, Запорожье, Украина;
- Назар Алисултанов, Назар Шапиро, Гедалья Айдаров, Султан Станбеков, Давид Миркин, Лия Тюлегенова и Талья Айдарова из Еврейской школы “ОРТ При Ец Хаим”,Бишкек, Кыргызстан;
- Арсений Зайков, Даниэль Лотоха, Миша Лисянский, Глеб Леницкий, Кира Шварц, Анастасия Танская и Анна Берлин из СШ “ОРТ” №94, Одесса, Украина.
Особенно хочется отметить Александру Гольдину (из СШ №41, Черновцы, Украина) и Давида Миркина (из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан) за присланные файлы с хорошим объяснением их решения.
К сожалению, не все участники поняли систему начисления баллов и мы получили много правильных ответов без всякого объяснения. В этом туре, мы решили дать 3 балла за правильный ответ и 4 балла за ответ с хорошим решением и объяснением.
Задание №4 (прием ответов до 23 декабря 2019)
| Группа из 12 человек (мужчин, женщин и детей) несёт 12 буханок хлеба. Каждый мужчина несёт 2 буханки, каждая женщина несёт 1/2 буханки и каждый ребёнок несёт 1/4 буханки хлеба. Сколько было в группе мужчин, женщин и детей? |
Решение задачи №4
Обозначим число мужчин в группе буквой Х, число женщин буквой Y и число детей буквой Z. |
Нами было получено 25 ответов, из которых 22 оказались правильными.
Правильные ответы (по школам в порядке очерёдности) прислали:
- Давид Циткилов и Захар Манелис из школы №1311, Москва, Россия;
- Илья Кузьмич и Даниэль Богович из Еврейской школы, Таллинн, Эстония;
- Анна Сечкина, Данил Авраменко и Егор Жоров из НКВ №141, Киев, Украина;
- Лирон Бланк и Марик Войцеховский из гимназии им. Шалом Алейхема, Вильнюс, Литва;
- Матвей Кушпарь из гимназии “ОРТ Алеф”, Запорожье, Украина;
- Александр Голецек из СШ №41, Черновцы, Украина;
- Гедалья Айдаров и Назар Шапиро из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Все они получают по 1 баллу.
Ответы с неполным решением (по школам в порядке очерёдности) прислали:
- Максим Вацко и Костя Ерёмин из НКВ №141, Киев, Украина;
- Аскольд Гальчук и Полина Грушевата из СШ №41, Черновцы, Украина;
- Евгения Лифшиц из школы им. Дубнова, Рига, Латвия;
- Назар Алисултанов и Маргарита Лавриненко из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Все они получают по 2 балла.
Полное решение прислали:
- Валерия Скакун из СШ №41, Черновцы, Украина;
- Давид Миркин из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Они получают по 3 балла.
Особенно хочется отметить Александру Гольдину из СШ №41, Черновцы, Украина за оригинальное (но неполное) решение, она получает дополнительный бонусный балл (всего 3 балла).
Задание №5 (прием ответов до 30 декабря 2019)
| После 7 стирок кусок хозяйственного мыла стал в два раза короче, в два раза уже и в два раза ниже.
На сколько стирок хватит оставшегося куска? |
Решение задачи №5
Обозначим длину куска мыла вначале буквой а, ширину куска мыла вначале буквой b и высоту куска мыла вначале буквой с. |
Нами было получено 14 ответов, из которых 11 оказались правильными.
Правильные ответы (по школам в порядке очерёдности) прислали:
- Назар Алисултанов из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Егор Жоров из НКВ №141, Киев, Украина;
Оба получают по 1 баллу.
Ответы с неполным решением (по школам в порядке очерёдности) прислал:
- Илья Кузьмич из Еврейской школы, Таллинн, Эстония;
Он получает 2 балла.
Полное решение прислали:
- Аскольд Гальчук, Валерия Скакун и Александра Гольдина из СШ №41, Черновцы, Украина;
- Маргарита Лавриненко, Дарья Непомнящая, Назар Шапиро и Давид Миркин из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Все они получают по 3 балла.
Особенно хочется отметить за творческое представление своего решения, Костю Ерёмина из НКВ №141, Киев, Украина. Он получает дополнительный бонусный балл (всего 4 балла).
Задание №6 (прием ответов до 20 января 2020)
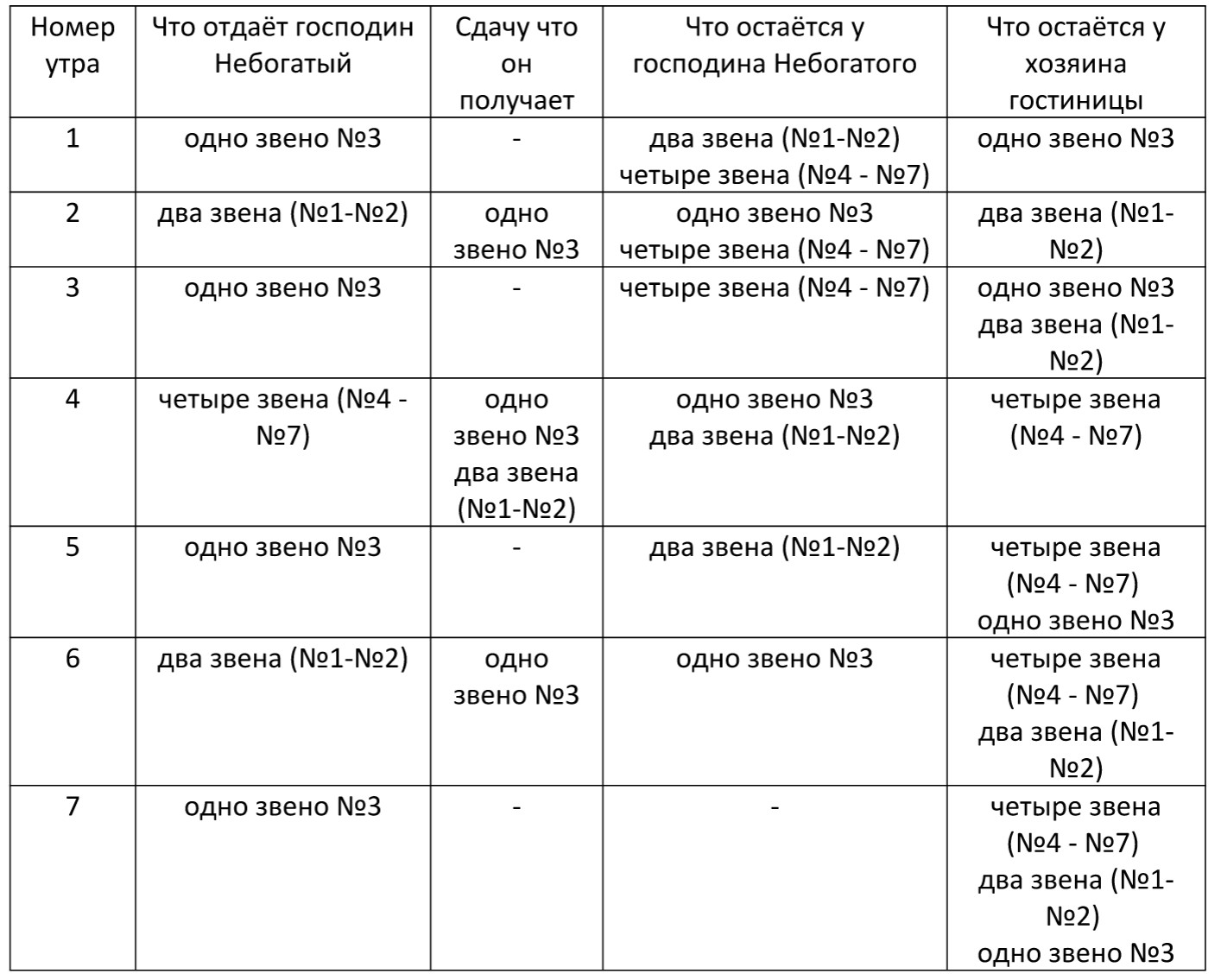
| Господин Небогатый приехал в город по делам, он должен был остаться там 8 дней (7 ночей). В городе была одна гостиница, но денег у него не было. Зато у него была красивая серебряная цепочка из 7 звеньев.
Хозяину гостиницы цепочка понравилась, и они договорились, что господин Небогатый расплатится цепочкой за своё проживание в гостинице. Но так как оплата в гостинице ежедневная хозяин выдвинул следующие требования: 1. каждое утро господин Небогатый должен отдать ему одно звено цепочки, как оплату за прошедшую ночь Как господину Небогатому выполнить эти условия и сколько разрезов нужно для этого сделать? |
Ответ на задачу:
Для того, чтобы выполнить условия хозяина гостиницы и прожить там 7 ночей, господин Небогатый должен сделать один разрез звена №3:
После этого цепочка распадётся на три части – одно звено №3 (которое было разрезано), два связанных звена (№1 и №2) и четыре связанных звена (№4 – №7).
Число звеньев цепочки, которые остаются у хозяина каждое утро, равно количеству ночей, которые провёл господин Небогатый в его гостинице. |
Нами было получено 13 решений, из которых 5 оказались полными и правильными.
Правильные решения (по школам в порядке очерёдности) прислали:
- Назар Алисултанов, Алиса Скоповская, Назар Шапиро и Давид Миркин из Еврейской
школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан; - Валерия Скакун из СШ №41, Черновцы, Украина;
Все они получают по 3 балла.
Задание №7 (прием ответов до 27 января 2020)
| Один мальчик решил принести своей бабушке несколько пирожных в честь её дня рождения. Бабушка живёт в другом конце города и по дороге к ней нужно пройти 7 мостов. На каждом мосту живёт голодный Серый Волк, он отбирает у мальчика половину пирожных, которые у него есть. Но если мальчик расскажет ему, что эти пирожные предназначены для бабушки, у которой сегодня день рождения, Серый Волк его пожалеет и отдаст ему одно пирожное назад.Сколько пирожных мальчик должен взять с собой из дома для того чтобы принести бабушке два пирожных? |
Решение задачи №7
Начнём решение задачи с конца – мальчику нужно уйти с седьмого моста с двумя пирожными. На этом мосте, одно пирожное он получил от Серого Волка (после того как отдал ему половину того что у него было), значит он пришёл на этот мост с двумя пирожными – одно он сразу отдал Серому Волку, а потом рассказав ему про бабушку получил одно пирожное назад. То есть если мальчик приходит на каждый мост с двумя пирожными, одно он вначале отдаёт, а потом, получает его обратно. В результате он и уходит с этого моста с двумя пирожными. Поэтому самое лучшее для него решение это выйти из дома с двумя пирожными и на каждом мосту рассказывать Серому Волку, что это пирожные для бабушки, у которой сегодня день рождения. |
Как правильно заметили Давид Миркин и Дарья Непомнящая (из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан), у задачи есть и другие решения. Эти решения естественно являются далеко не наилучшими. Так например, если мальчик не будет просить пирожные обратно, он может выйти из дома с 256 (28 = 256), на каждом мосту отдать половину и прийти к бабушке с 2 пирожными. В принципе, можно доказать, что выйдя из дома с любым количеством пирожных больше двух, (и прося пирожные обратно) у мальчика в конце останется больше 2 пирожных.
Нами было получено 16 ответов и решений, из которых 14 оказались правильными.
- Правильный ответ прислал Данил Авраменко из НКВ №141, Киев, Украина; он получает один балл.
Правильный ответ с неточным решением прислали:
- Матвей Кушпарь и Даниил Суханов из гимназии “ОРТ Алеф”, Запорожье, Украина.
Каждый ученик получает два балла.
Правильные ответы с полным решением (по школам в порядке очерёдности) прислали:
- Даниэль Богович и Илья Кузьмич из Еврейской школы, Таллинн, Эстония;
- Эвелина Грязева из гимназии “ОРТ Алеф”, Запорожье, Украина;
- Назар Алисултанов, Алиса Скоповская, Давид Миркин и Назар Шапиро из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Валерия Скакун и Аскольд Гальчук из СШ №41, Черновцы, Украина;
- Костя Ерёмин из НКВ №141, Киев, Украина;
Все они получают по 3 балла.
Хочется отметить Дарью Непомнящую из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан, которая прислала дополнительное возможное решение. К сожалению, в этом решении оказалась ошибка, и она тоже получает 3 балла.
Задание №8 (прием ответов до 03 февраля 2020)
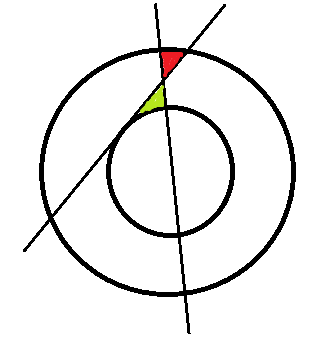
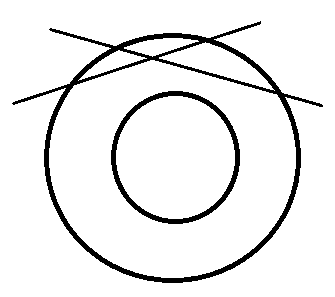
| Пять хороших друзей пошли погулять. По дороге они немного проголодались, но у них был один большой бублик.
Так как все были хорошими друзьями, и в разной мере голодными, они не возражали получить разного размера кусочки, но при этом они хотели разделить бублик при помощи всего двух разрезов. |
Решение задачи №8 Для правильного решения есть два условия:
|
Нами было получено 16 решений, из которых 12 оказались правильными.
Правильные решения (по школам в порядке очерёдности) прислали:
- Валерия Скакун, Полина Гушевата и Аскольд Гальчук из СШ №41, Черновцы, Украина;
- Бенайа Айдаров, Алиса Скоповская, Софья Мирошкина, Давид Миркин, Назар Шапиро и Султан Станбеков из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Все они получают по 3 балла.
Некоторые ученики правильно указали на условие №1 (пересечение разрезов на самом бублике), но к правильной формулировке второго условия ближе всего подошли:
- Даниэль Богович и Илья Кузьмич из Еврейской школы, Таллинн, Эстония;
Анна Сечкина из НКВ №141, Киев, Украина;
Они получают дополнительный бонусный балл и всего по 4 балла.
Задание №9 (прием ответов до 10 февраля 2020)
| В стране Тимбокту в ходу монеты 1 тимбоку, 3 тимбоку и 5 тимбоку.
Сможете ли вы разменять бумажную купюру в 200 тимбоку на монеты, так чтобы общее число монет было нечётным числом? |
Решение задачи №9:
Обозначим число монет номиналом в 1 тимбоку как k, номиналом в 3 тимбоку как m и номиналом в 5 тимбоку как n. Понятно что k, m, n целые и неотрицательные числа. |
Нами было получено 11 ответов и решений, из которых 10 оказались правильными.
Правильный ответ прислал:
- Даниэль Богович из Еврейской школы, Таллинн, Эстония; Он получает 1 балл.
Правильный ответ с частичным решением (по школам в порядке очерёдности) прислали:
- Илья Кузьмич из Еврейской школы, Таллинн, Эстония;
- Назар Алисултанов, Султан Станбеков, Дарья Непомнящая из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Костя Ерёмин из из НКВ №141, Киев, Украина;
Все они получают по 2 балла.
Полные решения прислали:
- Давид Миркин и Назар Шапиро из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Валерия Скакун из СШ №41, Черновцы, Украина;
К сожалению, решение Давида Миркина было не совсем точным и он получает 2 балла. Назар Шапиро из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан и Валерия Скакун из СШ №41, Черновцы, Украина получают по 3 балла за свои решения.
Красивое доказательство невозможности размена прислала Алиса Скоповская из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан. Она получает дополнительный бонусный балл и всего 4 балла.
Задание №10 (прием ответов до 17 февраля 2020)
Ювелир, механик и инженер имена которых (не обязательно в порядке их профессий!) Борис, Лёва и Миша встретились с аэропорту по пути в Тимбокту на летний отпуск. Из общего разговора выяснилось что:
Как зовут ювелира? |
Решение задачи №10 1. Если Борис и механик жили когда-то в посёлке Маленький, значит Борис не механик 2. Если ювелир и Лёва живут в одной стране, значит Лёва не ювелир 3. Если Миша моложе чем инженер, значит Миша не инженер 4. Если Лёва старше механика, значит Лёва не механик Если Лёва не ювелир и не механик, значит Лёва инженер. Борис не механик и не инженер, значит Борис ювелир. Ответ – ювелира зовут Борис. |
Нами было получено 14 ответов и решений, из которых 13 оказались правильными.
Правильный ответ прислал:
- Егор Жоров из НКВ №141, Киев, Украина;
Он получает 1 балл.
Правильный ответ с полным решением (по школам в порядке очерёдности) прислали:
- Илья Кузьмич и Даниэль Богович из Еврейской школы, Таллинн, Эстония;
- Назар Шапиро, Софья Ермошкина, Назар Алисултанов, Алиса Скоповская, Давид Миркин, Дарья Непомнящая из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Валерия Скакун, Полина Гушеватая и Александра Гольдина из СШ №41, Черновцы, Украина;
- Костя Ерёмин из НКВ №141, Киев, Украина;
Все они получают по 3 балла.
Задание №11 (прием ответов до 24 февраля 2020)
| Во время стоянки маленького корабля между двумя рейсами матросу исполнилось 20 лет. По этому случаю в каюте собрались все 6 членов команды. Я вдвое старше юнги и на 6 лет старше машиниста – сказал рулевой. А я на столько же лет старше юнги, на сколько моложе машиниста – заметил боцман. Кроме того я на 4 года старше матроса. Вы знаете, что средний возраст всей нашей команды 28 лет – сказал капитан. Сколько лет капитану? |
Ответ на задачу №11: Матросу 20 лет, и если боцман на 4 года его старше значит боцману 24 года. Обозначим возраст юнги за Х, а возраст машиниста за Y. По словам боцмана он на столько же лет старше юнги насколько моложе машиниста, значит: 24 – Х = Y – 24 По словам рулевого он вдвое старше юнги и на 6 лет старше машиниста, значит: 2Х = Y + 6 У нас есть 2 уравнения с двумя неизвестными: Х + Y = 48 2Х – Y = 6 Сложим эти два уравнения и получим 3Х = 54 и Х = 18. Подставим Х в первое уравнение и получим Y = 30. То есть юнге 18 лет, машинисту 30 лет, а рулевому 36 лет. Сумма возрастов юнги, матроса, боцмана, машиниста и рулевого: 18 + 20 + 24 + 30 + 36 = 128 Средний возраст всех 6 членов команды 28 лет, поэтому сумма их возрастов должна быть 28 х 6 = 168 Поэтому возраст капитана 168 – 128 = 40 лет. |
Нами было получено 9 правильных ответов и решений.
Правильный ответ прислала:
- Софья Ермошкина из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан; Она получает 1 балл.
- Правильный ответ с неполным решением прислал:
Илья Кузьмич из Еврейской школы, Таллинн, Эстония; Он получает 2 балла. - Правильный ответ с полным решением прислал:
Костя Ерёмин из НКВ №141, Киев, Украина;
К сожалению, в его решении была ошибка и он получает тоже 2 балла. - Правильный ответ с полным решением (по школам в порядке очерёдности) прислали:
Назар Шапиро, Алиса Скоповская и Давид Миркин из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Валерия Скакун и Полина Гушеватая из СШ №41, Черновцы, Украина;
Михайло Панасюк из НКВ №141, Киев, Украина;
Все они получают по 3 балла.
Задание №12 (прием ответов до 02 марта 2020)
| По дереву высотой 14 метров ползёт гусеница. За день она поднимается на 6 метров вверх, а за ночь сползает на 4 метра вниз.
Если гусеница начала ползти с земли, за сколько дней она попадёт на вершину дерева? |
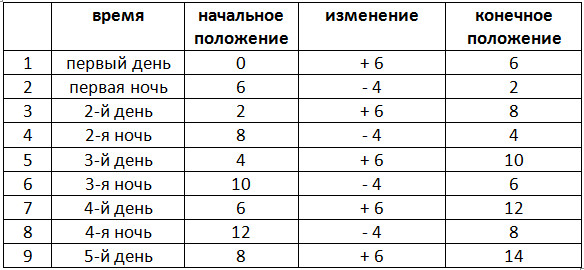
Ответ на задачу №12:
Опишем положение гусеницы в следующей таблице (все расстояния в метрах):
Так как высота дерева 14 метров, гусеница попадёт на вершину в конце пятого дня. |
Нами было получено 14 ответов и решений, из которых 11 оказались правильными.
Правильный ответ прислал:
- Егор Жоров из НКВ №141, Киев, Украина; Он получает 1 балл.
Правильный ответ с полным решением (по школам в порядке очерёдности) прислали:
- Даниил Суханов из гимназии “ОРТ Алеф”, Запорожье, Украина;
- Яша Доля и Иван Марков из Технологического лицея ОРТ имени Б. З. Герцля, Кишинёв, Молдова;
- Назар Шапиро, Алиса Скоповская, Давид Миркин и Дарья Непомнящая из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Аскольд Гальчук, Валерия Скакун и Александра Гольдина из СШ №41, Черновцы, Украина;
Все они получают по 3 балла.
Задание №13 (прием ответов до 09 марта 2020)
| Электропоезд длиной 20 метров проезжает мимо километрового столба за 2 секунды.
Если скорость поезда постоянна, то сколько времени ему понадобится, чтобы проехать мост длиной в 40 метров? |
Ответ на задачу №13:
Так как поезд длиной 20 метров, проезжает мимо столба за 2 секунды, скорость поезда: 20 м/ 2 сек = 10 м/сек Для того чтобы полностью проехать мост длиной в 40 метров локомотив поезда должен проехать 60 метров (40 метров длина моста + 20 метров длина поезда). Так как скорость поезда 10 м/сек это займёт: 60 м / 10 м/сек = 6 cекунд
|
Нами было получено 12 ответов и решений, из которых 9 оказались правильными.
Полное решение с маленькой ошибкой прислали:
- Яша Доля из Технологического лицея ОРТ имени Б. З. Герцля, Кишинёв, Молдова;
- Лия Тюлегенова из из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Они получают по 2 балла.
Правильный ответ с полным решением (по школам в порядке очерёдности) прислали:
- Назар Шапиро, Дарья Непомнящая, Алиса Скоповская и Давид Миркин из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Илья Кузьмич из Еврейской школы, Таллинн, Эстония;
- Валерия Скакун из СШ №41, Черновцы, Украина;
- Костя Ерёмин из НКВ №141, Киев, Украина;
Все они получают по 3 балла.
Задание №14 (прием ответов до 16 марта 2020)
| Натуральное число называется палиндромом, если его значение не меняется, когда мы читаем его справа налево. Так например, 12321 это палиндром, а 123456 нет.
Перед вами пример сложения: ** + *** = **** (каждая звёздочка обозначает какую-то цифру), в которой оба слагаемых и их сумма являются палиндромами. Не смогли бы вы найти решение этого примера? |
Решение задачи:
Нам известно что ** + *** = **** (каждая звёздочка обозначает какую-то цифру) и оба слагаемых и их сумма являются палиндромами. Понятно что сумма двухзначного и трёхзначного чисел будет вида 1aa1. Для того чтобы получить в сумме число больше 1000, трёхзначное число может быть только вида 9b9. То есть ** + 9b9 = 1aa1 . Поэтому двухзначное число может быть только 22 и мы имеем 22 + 9b9 = 1aa1 . Сейчас есть три возможности для цифры b: b =7 , b=8 или b=9. Если b =7 то мы получаем 22 + 979 = 1001 и все числа палиндромы. Если b =8 то мы получаем 22 + 989 = 1011 и сумма не является палиндромом. Если b =9 то мы получаем 22 + 999 = 1021 и сумма опять не является палиндромом. Поэтому единственное решение которое выполняет все условия: 22 + 979 = 1001 |
Нами было получено 12 ответов и решений и все они оказались правильными.
- Правильный ответ прислали:
Даниэль Богович и Илья Кузьмич из Еврейской школы, Таллинн, Эстония;
Карина Лунева из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Егор Жоров из НКВ №141, Киев, Украина;
Все они получают по 1 баллу. - Частичное решение прислала:
Лия Тюлегенова из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Она получает 2 балла. - Правильный ответ с полным решением (по школам в порядке очерёдности) прислали:
Назар Шапиро, Назар Алисултанов, Алиса Скоповская и Давид Миркин из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Костя Ерёмин из НКВ №141, Киев, Украина;
Валерия Скакун и Александра Гольдина из СШ №41, Черновцы, Украина;
Все они получают по 3 балла.
Задание №15 (прием ответов до 23 марта 2020)
| Перед нами три закрытые коробочки, в каждой лежит один маленький шарик белый, чёрный или зелёный. На каждой коробочке есть надпись: «белый», «чёрный», «или белый или зелёный», но ни одна из надписей не соответствует содержимому.
Не смогли бы вы определить какой шарик находится в каждой коробочке? |
Решение задачи 15:
Нам известно что:
Кроме того мы знаем что все надписи неправильные, поэтому в коробочке №3 («или белый или зелёный») может находиться только чёрный шарик:
Тогда белый шарик должен быть в коробочке №2 на которой написано «чёрный», а зелёный шарик будет тогда в коробочке №1.
|
Нами было получено 12 ответов и решений, из них 10 оказались правильными.
Полные правильные решения (по школам в порядке очерёдности) прислали:
- Валерия Скакун и Александра Гольдина из СШ №41, Черновцы, Украина;
- Карина Лунева, Алиса Скоповская, Назар Алисултанов, Давид Миркин и Назар Шапиро из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Костя Ерёмин из НКВ №141, Киев, Украина;
- Иван Марков из Технологического лицея ОРТ имени Б. З. Герцля, Кишинёв, Молдова;
- Илья Кузьмич из Еврейской школы, Таллинн, Эстония;
Все они получают по 3 балла.
Задание №16 (прием ответов до 30 марта 2020)
| Ученик купил 4 разные тетради. Все тетради без первой стоят 42 рубля, все без второй – 40 рублей, все без третьей – 38 рублей и все без четвёртой – 36 рублей.
Сколько стоит каждая тетрадь? |
Решение задачи:
Обозначим стоимости тетрадей: Х1 – первая тетрадь, Х2 – вторая тетрадь, Х3 – третья тетрадь, Х4 – четвёртая тетрадь По условиям задачи мы сможем составить следующие уравнения:
У нас есть простая система из четырёх уравнений с четырьмя неизвестными, и есть несколько способов её решить. Самый простой это сложить все уравнения, мы получим: 3Х1 + 3Х2 + 3Х3 + 3Х4 = 156 или 3(Х1 + Х2 + Х3 + Х4 ) = 156; разделим на 3 и получим: Х1 + Х2 + Х3 + Х4 = 52 То есть стоимость всех четырёх тетрадей 52 рубля. Поэтому стоимость каждой тетради:
|
Нами было получено 10 ответов и решений, все они оказались правильными.
- Правильный ответ, но без объяснения прислала Даана Салиева из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан; Она получает 1 балл.
Полные правильные решения (по школам в порядке очерёдности) прислали:
- Илья Кузьмич из Еврейской школы, Таллинн, Эстония;
- Валерия Скакун из СШ №41, Черновцы, Украина;
- Дарья Непомнящая, Алиса Скоповская, Назар Шапиро, Лия Тюлегенова, Давид Миркин и Назар Алисултанов из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Костя Ерёмин из НКВ №141, Киев, Украина;
Все они получают по 3 балла.
Задание №17 (прием ответов до 06 апреля 2020)
| Ира, Даша, Миша и Боря собирали грибы в лесу.
Ира собрала больше всех грибов, а Даша не меньше всех. Верно ли что девочки собрали больше грибов, чем мальчики? |
Решение задачи:
Обозначим сколько грибов собрал каждый из ребят: Х1 – Ира, Х2 – Даша, Y1 – Миша, Y2 – Боря По условиям задачи мы знаем что Ира собрала больше всех грибов, а Даша не меньше всех. То есть Х1 > Х2, Y1, Y2 и у нас есть несколько возможностей:
Тогда может быть Х2 ≥ Y1 > Y2 или Y1 > Х2 ≥ Y2 В любом из этих случаев так как Х1 > Y1 и Х2 ≥ Y2 то Х1 + Х2 > Y1 + Y2
Тогда опять может быть Х2 > Y1 = Y2 или Х2 = Y1 = Y2 В любом из этих случаев Х2 ≥ Y1 = Y2 И поэтому опять, так как Х1 > Y1 и Х2 ≥ Y2 то Х1 + Х2 > Y1 + Y2 То есть в любом случае девочки собрали больше грибов чем мальчики. |
Нами было получено 9 ответов и решений, все они оказались правильными.
Правильный ответ, но без решения прислала Даана Салиева из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Правильный ответ (с не очень понятным объяснением) прислал Костя Ерёмин из НКВ №141, Киев, Украина;
Они получают по 1 баллу.
Полные правильные решения (по школам в порядке очерёдности) прислали:
Алиса Скоповская, Давид Миркин, Назар Шапиро, Назар Алисултанов и Дарья Непомнящая из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Даниэль Богович из Еврейской школы, Таллинн, Эстония;
Валерия Скакун из СШ №41, Черновцы, Украина;
Все они получают по 3 балла.
Задание №18 (прием ответов до 13 апреля 2020)
| В погребе 20 одинаковых на вид банок с вареньем. В 8 банках клубничное варенье, в 7 банках малиновое варенье и в 5 банках вишнёвое варенье.
Каково наибольшее количество банок, которые можно вынести в темноте из погреба с уверенностью, что там остались хотя бы ещё 4 банки одного сорта варенья и 3 банки другого сорта? |
Решение задачи: Для решения задачи должны соблюдаться два условия:
Для описания ситуации введём обозначение – (количество банок клубничного варенья, количество банок малинового варенья, количество банок вишнёвого варенья). Наше начальное положение – (8, 7, 5). Понятно что мы не можем забрать из погреба 12 банок варенья, так как может случится что мы возмём все банки малинового и вишнёвого варенья и тогда получится:
Если мы попытаемся взять 11 банок то может получится:
Если мы попытаемся взять 10 банок то может получится:
Попробуем взять 9 банок, но тогда может получится:
Попробуем взять 8 банок, но тогда может получится:
Но если мы возмём 7 банок, то легко убедится что оба условия будут соблюдены. Поэтому максимальное число банок варенья, которые можно взять из погреба равно 7. |
Нами было получено 7 решений, все они оказались правильными.
Полные правильные решения (по школам в порядке очерёдности) прислали:
Алиса Скоповская, Давид Миркин, Назар Алисултанов, Назар Шапиро и Дарья Непомнящая из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан; Валерия Скакун из СШ №41, Черновцы, Украина;
Костя Ерёмин из НКВ №141, Киев, Украина;
Все они получают по 3 балла.
Задание №19 (прием ответов до 20 апреля 2020)
| У некоторых натуральных чисел есть интересное свойство: если мы умножим это число на два то мы получим квадрат другого числа, а если мы умножим это число на три то получим куб ещё одного числа.
Не смогли бы вы найти минимальное натуральное число у которого есть такое свойство? |
Решение задачи: Обозначим наше число как Х, тогда по условиям задачи: 2Х = n2 и 3Х = s3 (Х ≠ n; Х ≠ s) Из последних уравнений понятно, что n должно делиться на 2 и s должно делиться на 3. То есть n = 2m и s = 3t; подставим n и s в наши уравнения и получим: 2Х = (2m)2 то есть 2Х = 4m2 и Х = 2m2 3Х = (3t)3 то есть 3Х = 27t3 и Х = 9t3 Мы получили что: 2m2 = 9t3 ; из этого уравнения понятно что m должно делиться на 3 и t должно делиться на 2. То есть m = 3k и t = 2u; подставим эти m и t в последнее уравнение и получим: 2(3k) 2 = 9(2u) 3 то есть 2(9k2) = 9(8u3) , и после сокращений получим k2 = 4u3 (*) Мы ищем минимальное решение данного уравнения в натуральных числах поэтому: k = 2 и u = 1, и поэтому m = 3k = 6 и t = 2u = 2 Х = 2m2 то есть Х = 2(6)2 = 72 (или Х = 9t3 то есть Х = 9(2)3 = 72) Данный метод решения позволяет найти и последующие натуральные числа обладающие этим свойством. Так например, вторым решением уравнения (*) будет k = 16 и u = 4 и соответственно m = 3k = 48 и Х = 2m2 то есть Х = 2(48)2 = 4608 . Третьим решением уравнения (*) будет k = 54 и u = 9 и соответственно m = 3k = 162 и Х = 2m2 то есть Х = 2(162)2 = 52488 и так далее. |
Было получено 7 ответов и решений, 6 из них оказались правильными.
Правильный ответ (но без объяснения) прислала: Дарья Непомнящая из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан; Она получает 1 балл.
Правильный ответ с частичным объяснением прислали:
- Костя Ерёмин из НКВ №141, Киев, Украина;
- Назар Алисултанов из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
Они получают по 2 балла.
Правильные решения с полным объяснением (по школам в порядке очерёдности) прислали:
- Назар Шапиро и Алиса Скоповская из Еврейской школы “ОРТ При Ец Хаим”, Бишкек, Кыргызстан;
- Александра Гольдина из СШ №41, Черновцы, Украина;
Все они получают по 3 балла.