Результати конкурсу у 2018-2019 навчальному році (5 найкращих участників):
| Місце | Учень | Школа | Результат |
| 1-2 | Іван Марков | Технологічний ліцей ГРТ імені Б. 3. Герцля, Кишинів, Молдова | 3,5 |
| 1-2 | Лірон Бланк | Гімназія ОРТ імені Ш. Алейхема, Вільнюс, Литва | 3,5 |
| 3-5 | Саша Урсу | Технологічний ліцей ОРТ імені Б. 3. Герцля, Кишинів, Молдова | 3 |
| 3-5 | Султан Станбеков | Єврейська школа “ОРТ – Прі Ец Хаїм”, Бішкек, Киргизстан | 3 |
| 3-5 | Назар Алісултанов | Єврейська школа “ОРТ – Прі Ец Хаїм”, Бішкек, Киргизстан | 3 |
КОНКУРСНІ ЗАВДАННЯ
Завдання №1 (прийом відповідей до 06 травня 2019)
Завдання запропоноване учнями єврейської школи “ОРТ-Прі Ец Хаїм” з міста Бішкек, Киргизстан.
Правильну відповідь надіслав Іван Марков із Технологічного ліцею ОРТ імені Б. З. Герцля, Кишинів, Молдова.
Завдання №2 (прийом відповідей до 13 травня 2019 року)
Завдання запропоноване учнями Єврейської школи з міста Таллінна, Естонія.
Правильні (але неповні) відповіді надіслали: Сашко Урсу та Аркадій Юсов із Технологічного ліцею ОРТ імені Б. З. Герцля, Кишинів, Молдова; Марік Войцеховський та Єва Радавічуйте з гімназії імені Ш. Алейхем з Вільнюса, Литва.
Завдання №3 (прийом відповідей до 20 травня 2019 року)
Не змогли б ви розрізати цю фігуру на дві однакові частини і за площею, і за формою?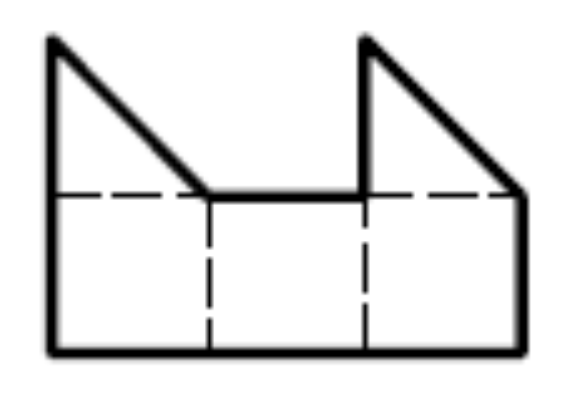 Розв’язання задачі №3: Розв’язання задачі №3: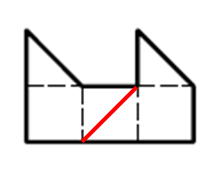 |

|
Правильне рішення надіслав Лірон Бланк із гімназії імені Ш. Алейхем з Вільнюса, Литва.
Завдання №4 (прийом відповідей до 27 травня 2019 року)
Правильну відповідь із поясненням надіслав Саша Урсу з ліцею ОРТ імені Б. З. Герцля з Кишинева, Молдова.
Правильні рішення надіслали Станбеков Султан, Давид Міркін, Лія Тюлегенова, Маргарита Лавриненко, Назар Алісултанов, Дар’я Непомнящая, Василина, Гедалія та Михайло Васильєв із єврейської школи “ОРТ-Прі Ец Хаїм”, з міста Бішкек, Киргизстан; Єва Радавічуйте, Лірон Бланк та Мантас Грюсаускас із гімназії імені Ш. Алейхема із Вільнюса, Литва; Андрій Гаркушин, Вікторія Куляк, Іван Марков, Юрій Мирон та Давид Гельван із ліцею ОРТ імені Б. З. Герцля з Кишинева, Молдова.
Правильне, але неповне рішення надіслав Міхаель Ільмер із єврейської школи “ОРТ-Прі Ец Хаїм”, з міста Бішкек, Киргизстан.
Завдання №5 (прийом відповідей до 03 червня 2019 року)
Правильну відповідь з неповним поясненням надіслали Султан Станбеков, Назар Алісултанов та Назар Шапіро з єврейської школи “ОРТ-Прі Ец Хаїм”, з міста Бішкек, Киргизстан.
Правильну відповідь надіслали Давид Міркін і Дар’я Непомняща з єврейської школи “ОРТ-Прі Ец Хаїм”, з міста Бішкек, Киргизстан; Марік Войцеховський із гімназії імені Ш. Алейхем з Вільнюса, Литва.
Не зовсім правильне рішення надіслали Лія Тюлегенова та Михайло Васильєв із єврейської школи “ОРТ-Прі Ец Хаїм”, з міста Бішкек, Киргизстан.


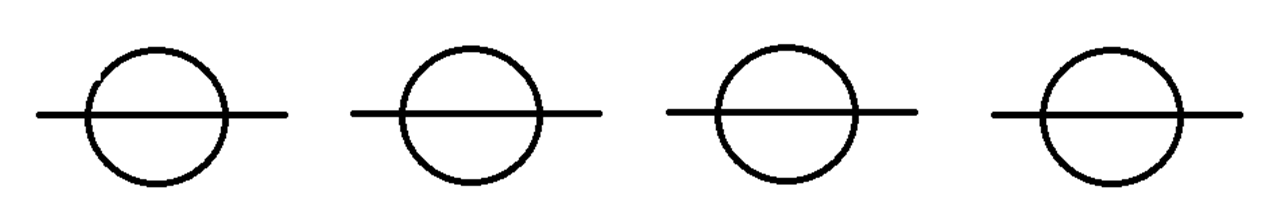 Останній п’ятий торт ми розріжемо на 8 рівних частин, і для цього нам доведеться зробити ще 4 розрізи.
Останній п’ятий торт ми розріжемо на 8 рівних частин, і для цього нам доведеться зробити ще 4 розрізи.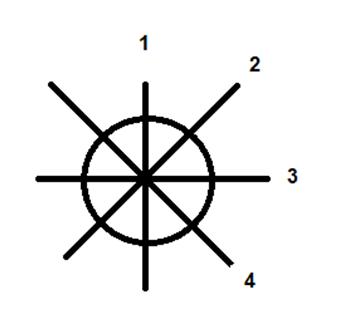 Кожен із друзів отримає по половині торта та 1/8, всього ми зробили для цього 8 розрізів.
Кожен із друзів отримає по половині торта та 1/8, всього ми зробили для цього 8 розрізів.